Dark-Existed's Blog

$\mathcal{O}_{i}=\sum_{j} \frac{\mathcal{S}\left(Q_{i}, K_{j}\right)}{\sum_{j} \mathcal{S}\left(Q_{i}, K_{j}\right)} V_{j}$

首先，为了解决时间空间复杂度是平方的问题。
通过之前的研究，可以有这种方法。

$\mathcal{S}\left(Q_{i}, K_{j}\right)=\phi\left(Q_{i}\right) \phi\left(K_{j}\right)^{T}$

$O_{i}=\frac{\sum_{j=1}^{N}\left(\phi\left(Q_{i}\right) \phi\left(K_{j}\right)^{T}\right) V_{j}}{\sum_{j=1}^{N}\left(\phi\left(Q_{i}\right) \phi\left(K_{j}\right)^{T}\right)}$

$\left(\phi(Q) \phi(K)^{T}\right) V=\phi(Q)\left(\phi(K)^{T} V\right)$

就是找到合适的核函数 $\phi$ 来模拟逼近 Softmax

由于矩阵的运算顺序变得可交换，来缩小运算量

使用了这几种来做对比

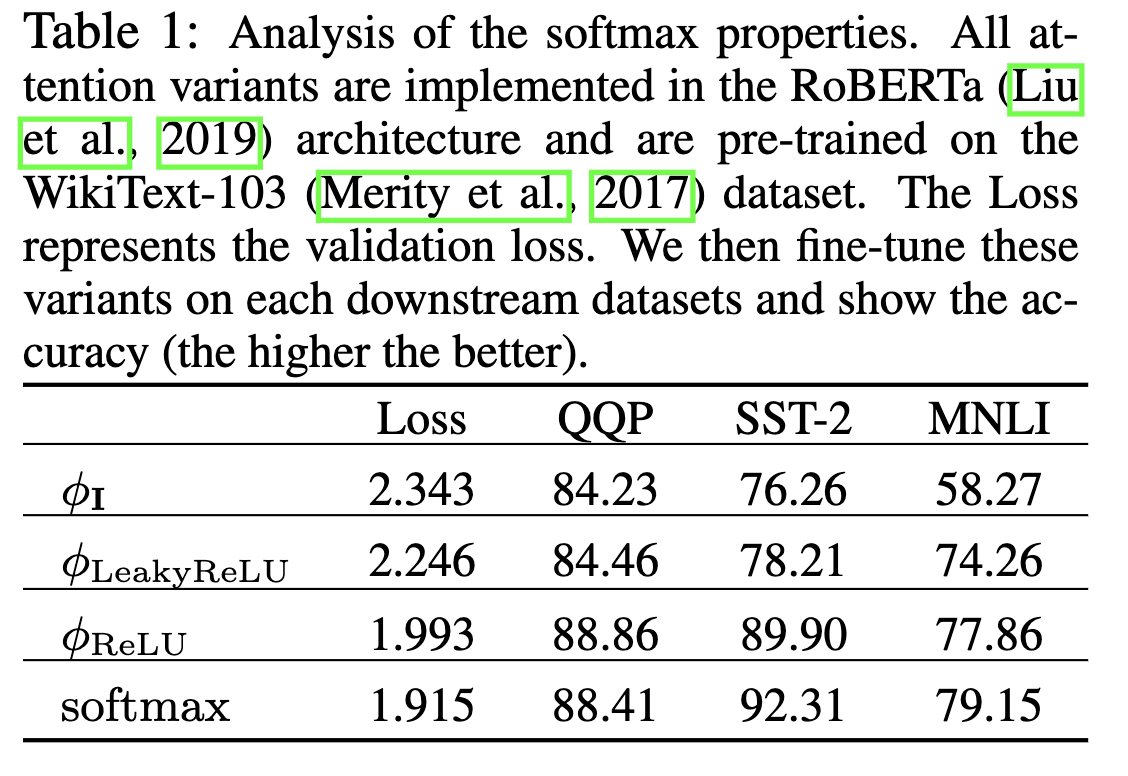
所以本文最后选取了 ReLU

$\mathcal{S}(Q, K)=\mathrm{s}\left(\phi_{\text {linear }}(Q), \phi_{\text {linear }}(K)\right)=\mathrm{s}\left(Q^{\prime}, K^{\prime}\right)$

$\phi_{\text {linear }}(x)=\operatorname{ReLU}(x)$

$\mathcal{O}_{i}=\frac{\sum_{j=1}^{N} f\left(\phi_{\text {linear }}\left(Q_{i}\right), \phi_{\text {linear }}\left(K_{j}\right)\right) V_{j}}{\sum_{j=1}^{N} f\left(\phi_{\text {linear }}\left(Q_{i}\right), \phi_{\text {linear }}\left(K_{j}\right)\right)}=\frac{\sum_{j=1}^{N}\left(\operatorname{ReLU}\left(Q_{i}\right) \operatorname{ReLU}\left(K_{j}\right)^{T}\right) V_{j}}{\sum_{j=1}^{N}\left(\operatorname{ReLU}\left(Q_{i}\right) \operatorname{ReLU}\left(K_{j}\right)^{T}\right)}$

$\mathcal{O}_{i}=\frac{\operatorname{ReLU}\left(Q_{i}\right) \sum_{j=1}^{N} \operatorname{ReLU}\left(K_{j}\right)^{T} V_{j}}{\operatorname{ReLU}\left(Q_{i}\right) \sum_{j=1}^{N} \operatorname{ReLU}\left(K_{j}\right)^{T}}$

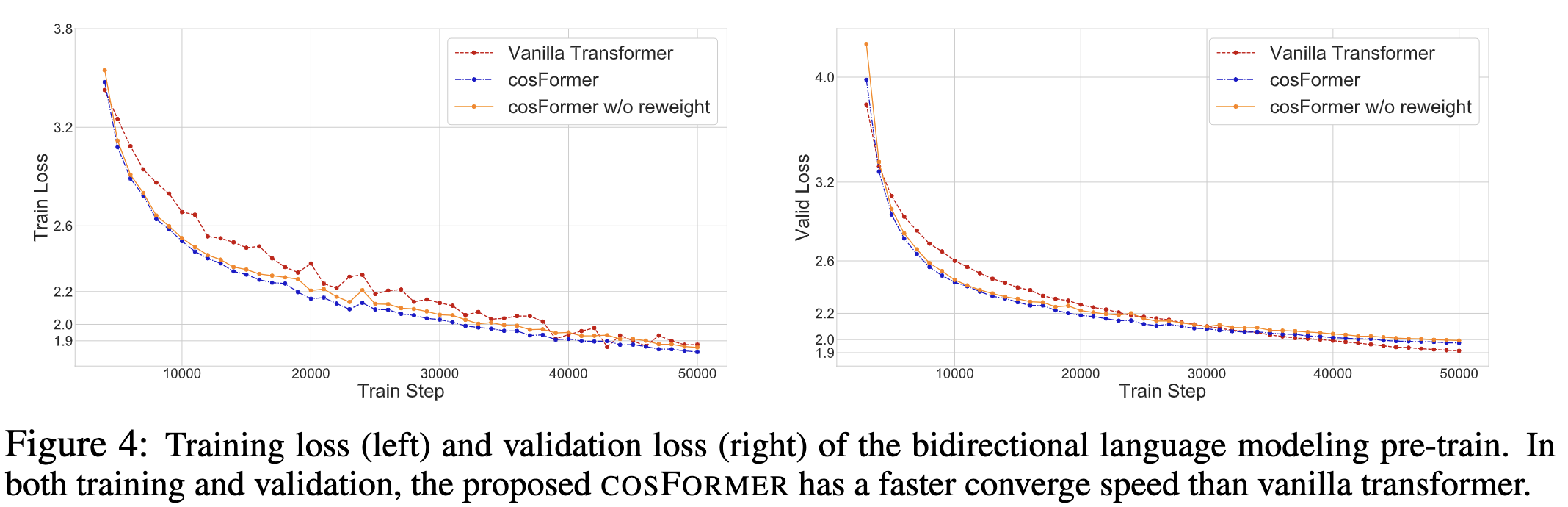
在 Softmax 注意力中引入非线性重加权机制可以聚集注意力权重的分布，因而稳定训练过程。研究者还通过实证发现，这种做法可以惩罚远距离连接，并在某些情况下加强局部性。

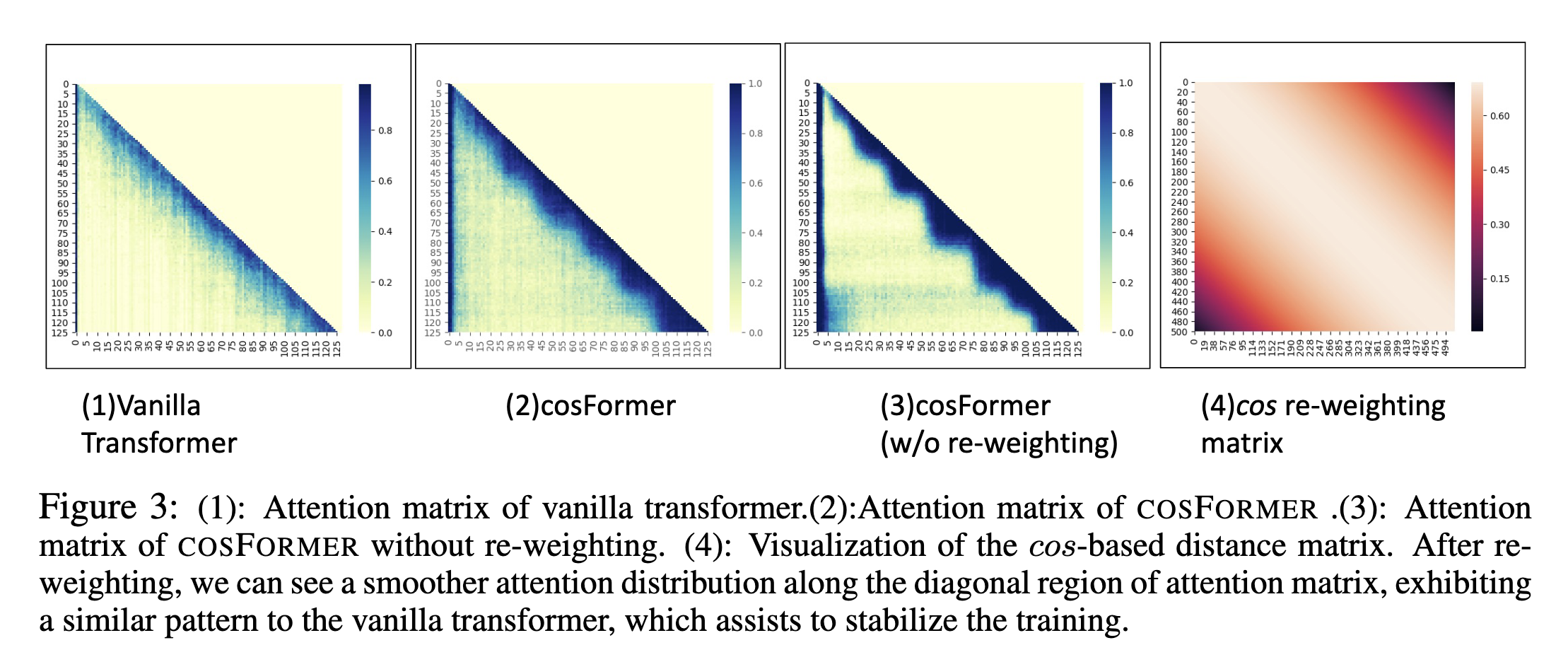
所以需要加强局部性，提出一种 re-weight 方法来加强。

$s\left(Q_{i}^{\prime}, K_{j}^{\prime}\right)=Q_{i}^{\prime} K_{j}^{\prime T} \cos \left(\frac{\pi}{2} \times \frac{i-j}{M}\right)$

$\begin{aligned} Q_{i}^{\prime} K_{j}^{\prime} \cos \left(\frac{\pi}{2} \times \frac{i-j}{M}\right) &=Q_{i}^{\prime} K_{j}^{\prime T}\left(\cos \left(\frac{\pi i}{2 M}\right) \cos \left(\frac{\pi j}{2 M}\right)+\sin \left(\frac{\pi i}{2 M}\right) \sin \left(\frac{\pi j}{2 M}\right)\right) \\ &=\left(Q_{i}^{\prime} \cos \left(\frac{\pi i}{2 M}\right)\right)\left(K_{j}^{\prime} \cos \left(\frac{\pi j}{2 M}\right)\right)^{T}+\left(Q_{i}^{\prime} \sin \left(\frac{\pi i}{2 M}\right)\right)\left(K_{j}^{\prime} \sin \left(\frac{\pi j}{2 M}\right)\right)^{T} \end{aligned}$

$O_{i}=\frac{\sum_{j=1}^{N} f\left(Q_{i}^{\prime}, K_{j}^{\prime}\right) V_{j}}{\sum_{j=1}^{N} f\left(Q_{i}^{\prime}, K_{j}^{\prime}\right)}=\frac{\sum_{j=1}^{N} Q_{i}^{\cos }\left(\left(K_{j}^{\cos }\right)^{T} V_{j}\right)+\sum_{j=1}^{N} Q_{i}^{\sin }\left(\left(K_{j}^{\sin }\right)^{T} V_{j}\right)}{\sum_{j=1}^{N} Q_{i}^{\cos }\left(K_{j}^{\cos }\right)^{T}+\sum_{j=1}^{N} Q_{i}^{\sin }\left(K_{j}^{\sin }\right)^{T}}$

$\mathcal{O}=\mathcal{S}(Q, K) V=\left(Q^{\cos } K^{\cos }+Q^{\sin } K^{\sin }\right) V=Q^{\cos }\left(K^{\cos } V\right)+Q^{\sin }\left(K^{\sin } V\right)$

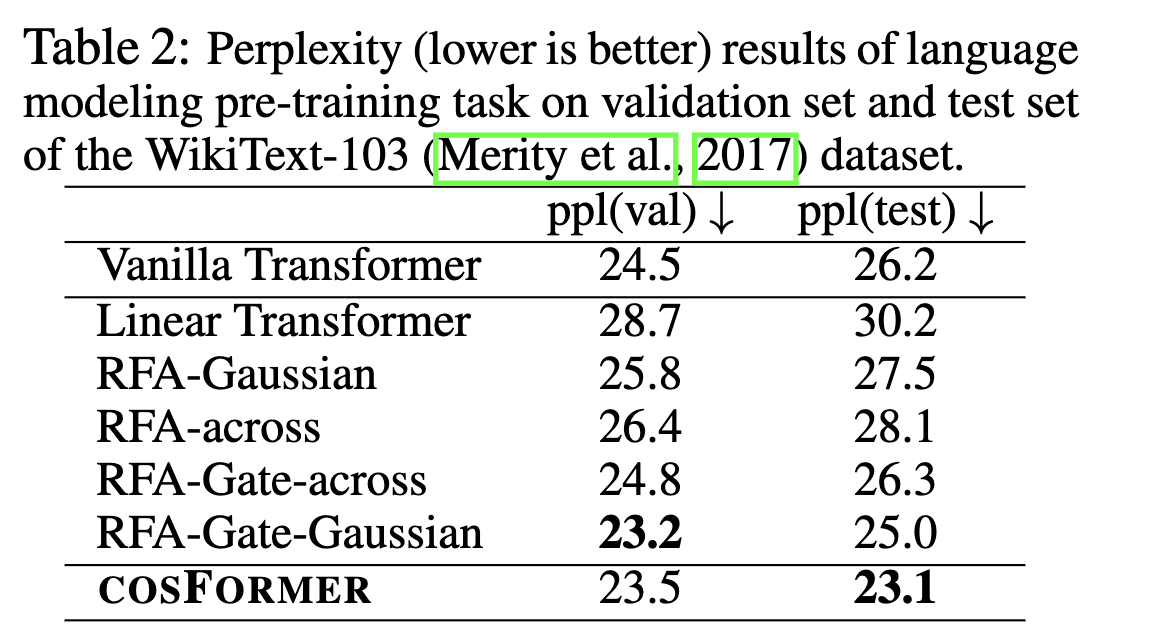
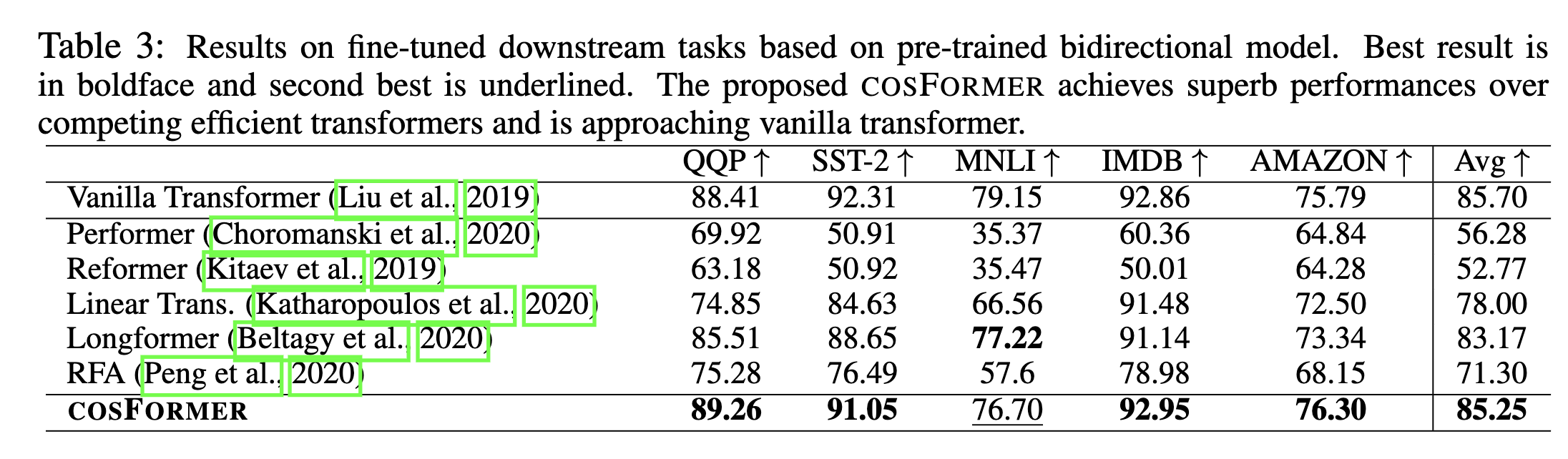
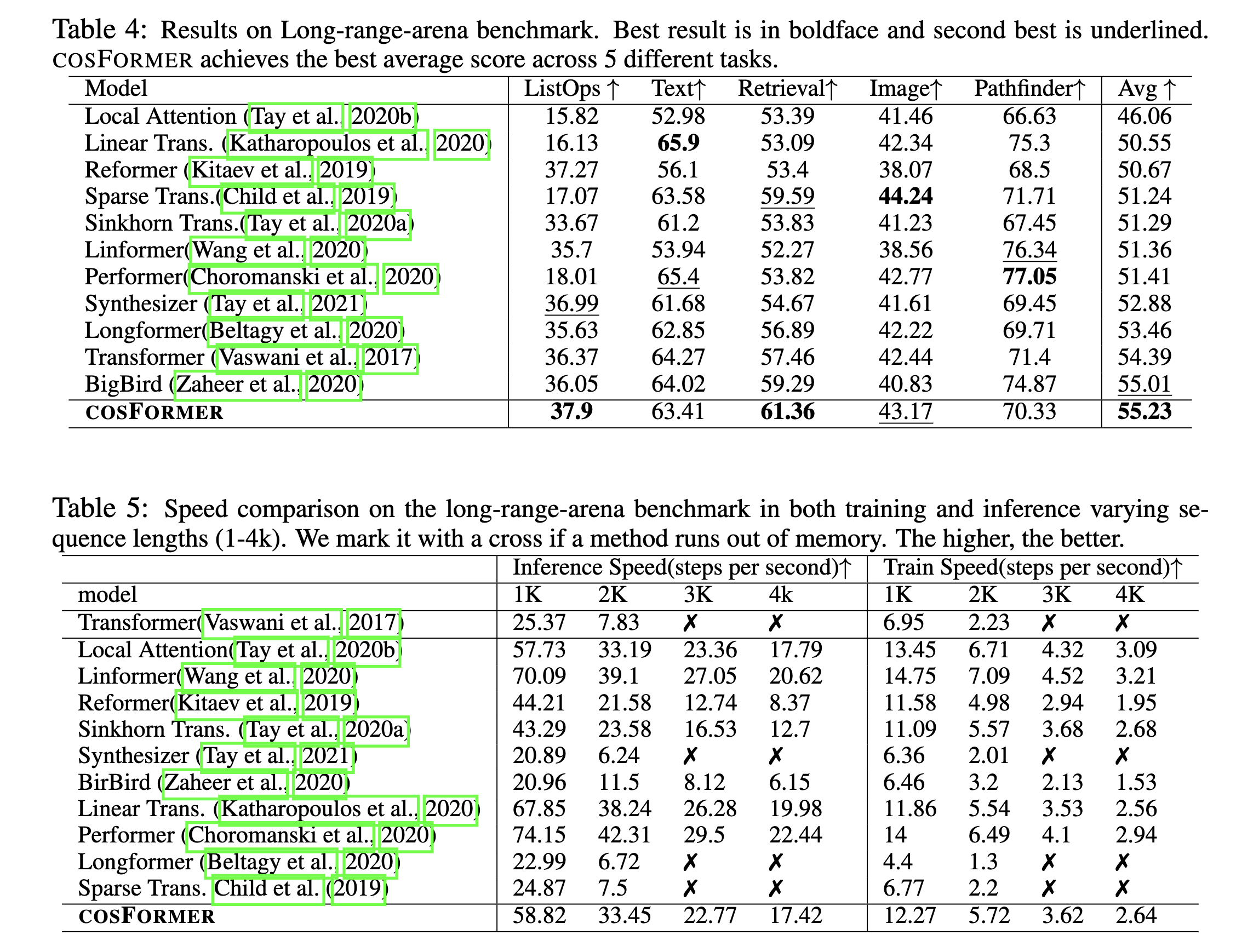
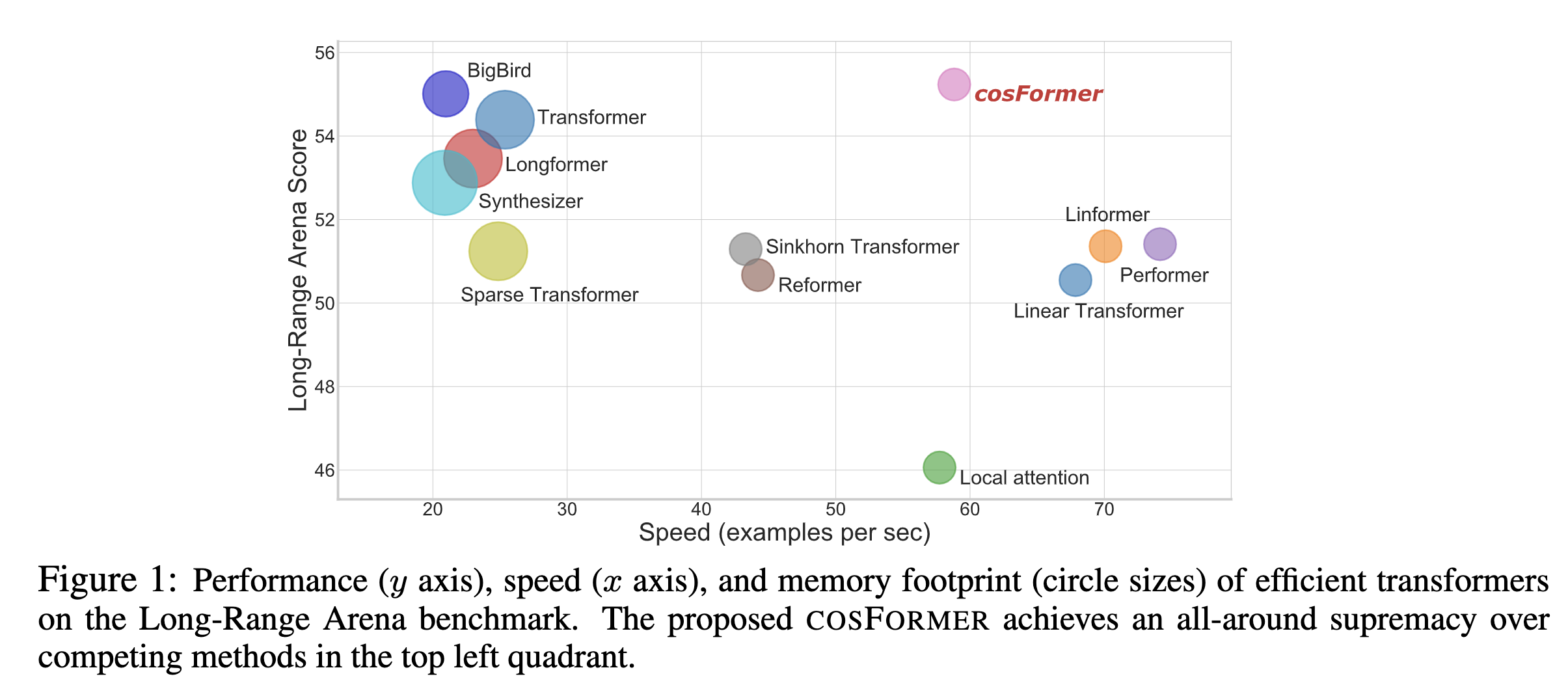
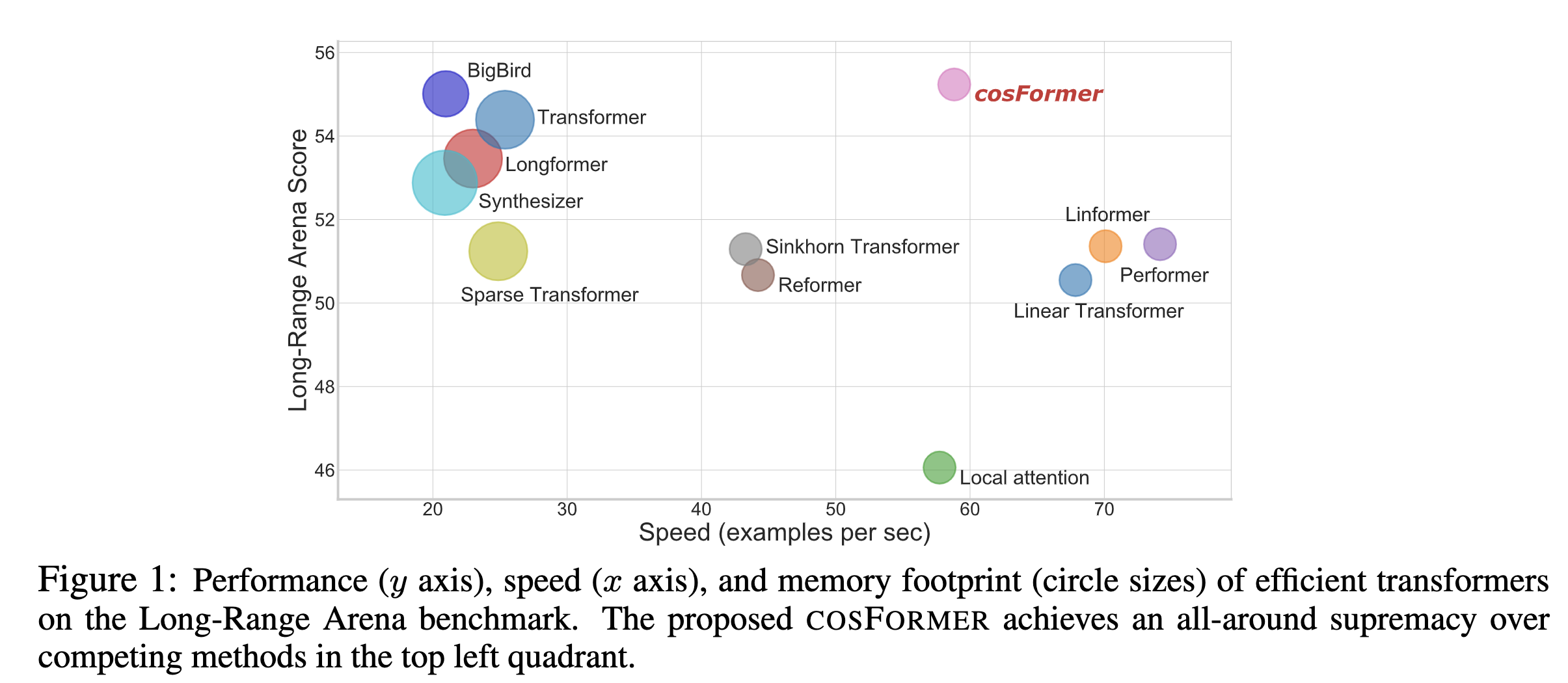
也通过实验来验证了 这种做法的有效性。

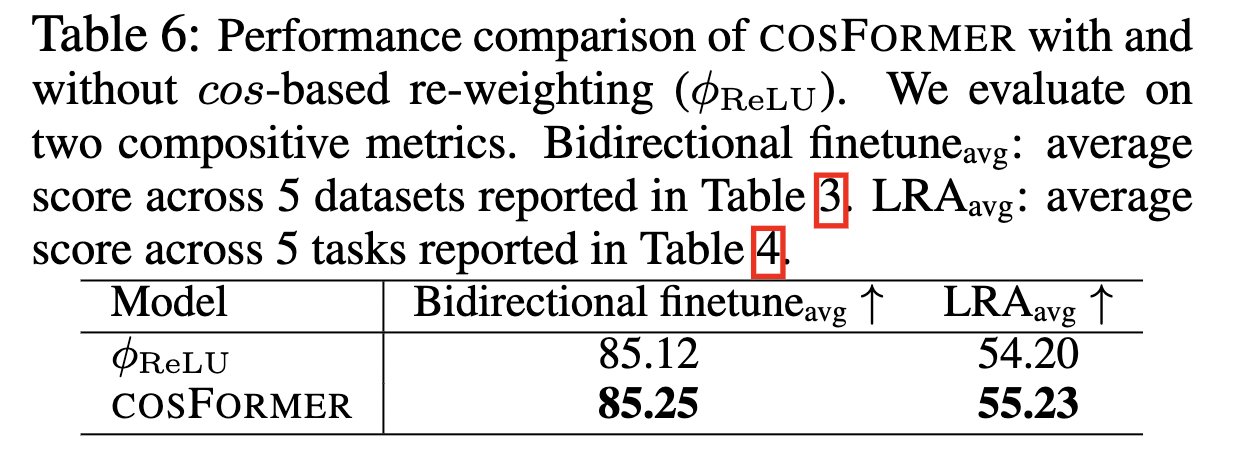
最后效果如下