Dark-Existed's Blog

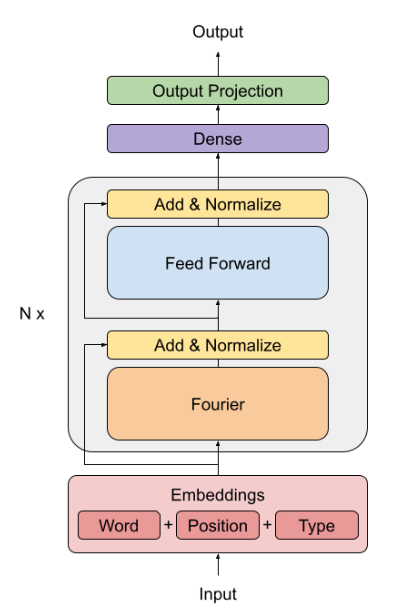
用傅里叶变换替换了 Self-Attention

首先，本论文通过他人的实验举例，说明Self-Attention中如果将权重冻结，使用高斯分布随机初始化，最终也能得到不错的效果。

由此可以尝试使用傅里叶变换替换此部分，从而解决 $O(n^2)$ 的问题。

通过实验发现去掉傅里叶变换的虚部的结果更好，所以没有使用原版的傅里叶变换。

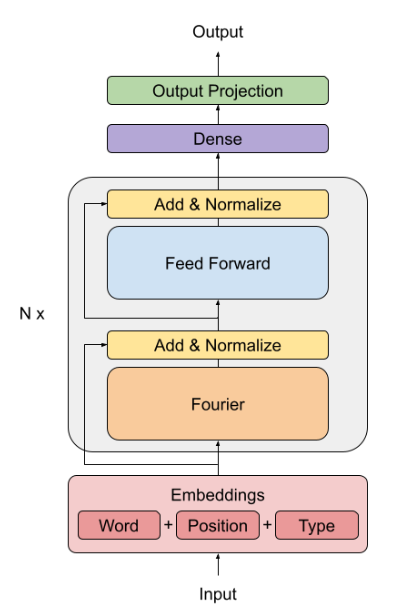
与 Self-Attention 相同，可以让后面的部分获得所有 token 的信息。

• 具体细节是 先沿着 hidden dimension 施加 1D 傅里叶变换，再向 sequence length dimension 施加傅立叶变换。

$y=\Re\left(\mathcal{F}_{\text {seq }}\left(\mathcal{F}_{\text {hidden }}(x)\right)\right)$

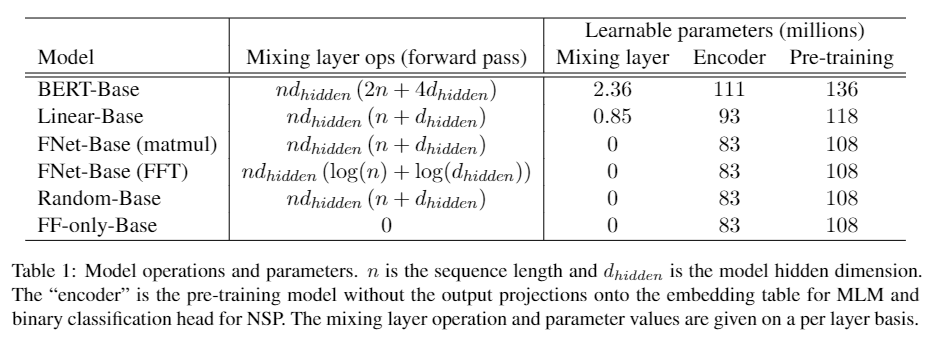
做了以下几种模型

1. BERT-BASE
2. FNet-encoder : 将每个 self-attention 都替换成 上文描述的傅里叶变换
3. Linear encoder : 将每个 self-attention 都替换成 两个 learnable, dense, linear sublayers ，分别施加在 hidden dimension 和 sequence length dimension
4. Random encoder : 将每个 self-attention 替换成随机初始化的矩阵，参数不可训练， 分别施加在 hidden dimension 和 sequence length dimension
5. Feed Forward-only (FF-only) encoder : 直接去掉 self-attention

参数量对比

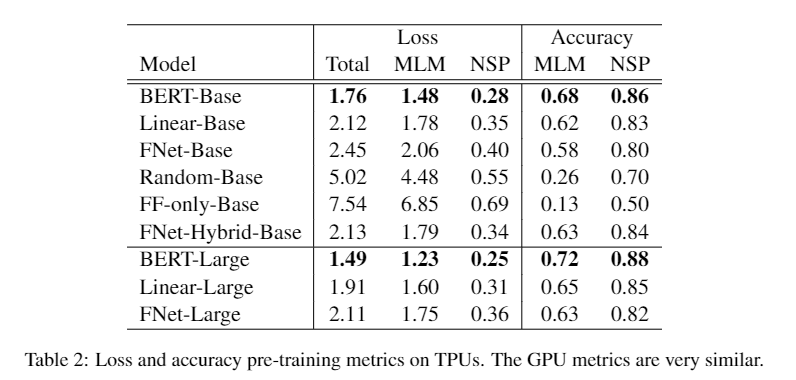
训练结果对比

FNet-Hybrid-Base 是把最后两层的傅里叶变换换成了 self-attention

速度对比

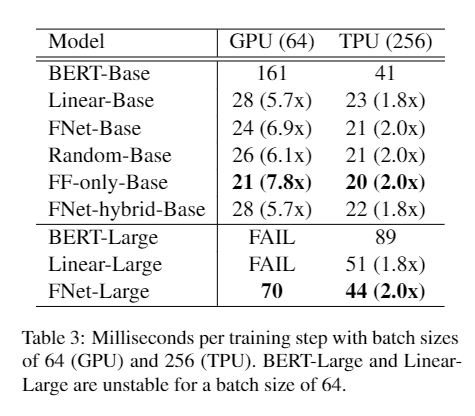
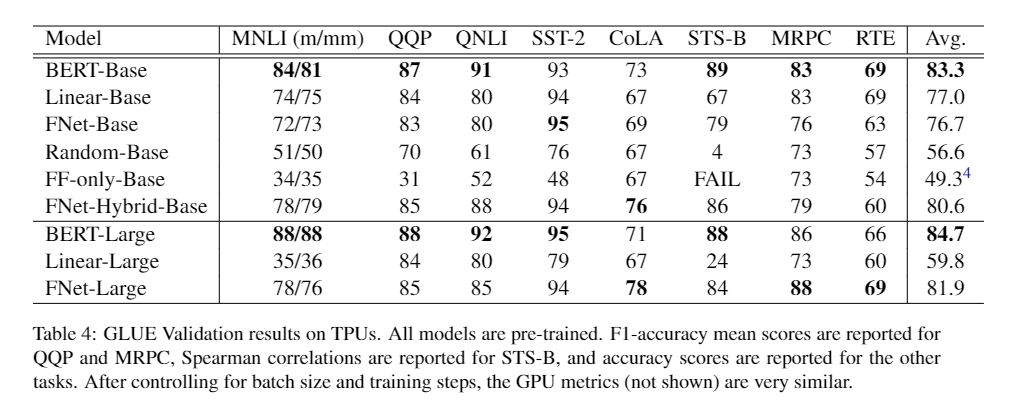
总结以下该篇论文：

1. 个人认为一般般，没什么很出色的亮点。 速度虽然说快了不少，但是效果也降了挺多 。
2. 本文中说 Linear encoder 虽然准确高了，但是训练过程中比较不稳定，然后在GPU上比较慢，内存占用比较大。不稳定的问题的话，个人观点是，没有对输出结果加约束，导致训练过程中，值的变换比较大，从而出现训练中不稳定的结果。可以使用某些约束来控制参数中的值的范围，使训练稳定下来。
3. 本文的一个观点是，self-attention 并不是说非常重要，只要有这么个可以混合全局信息的变换就行，想要提高速度，就换成一个其他的快一点的变换。所以个人的想法是，既然傅里叶变换可以，那只要找到个速度快，输出值的范围比较稳定的变换，达到的效果也能差不多的。