Dark-Existed's Blog

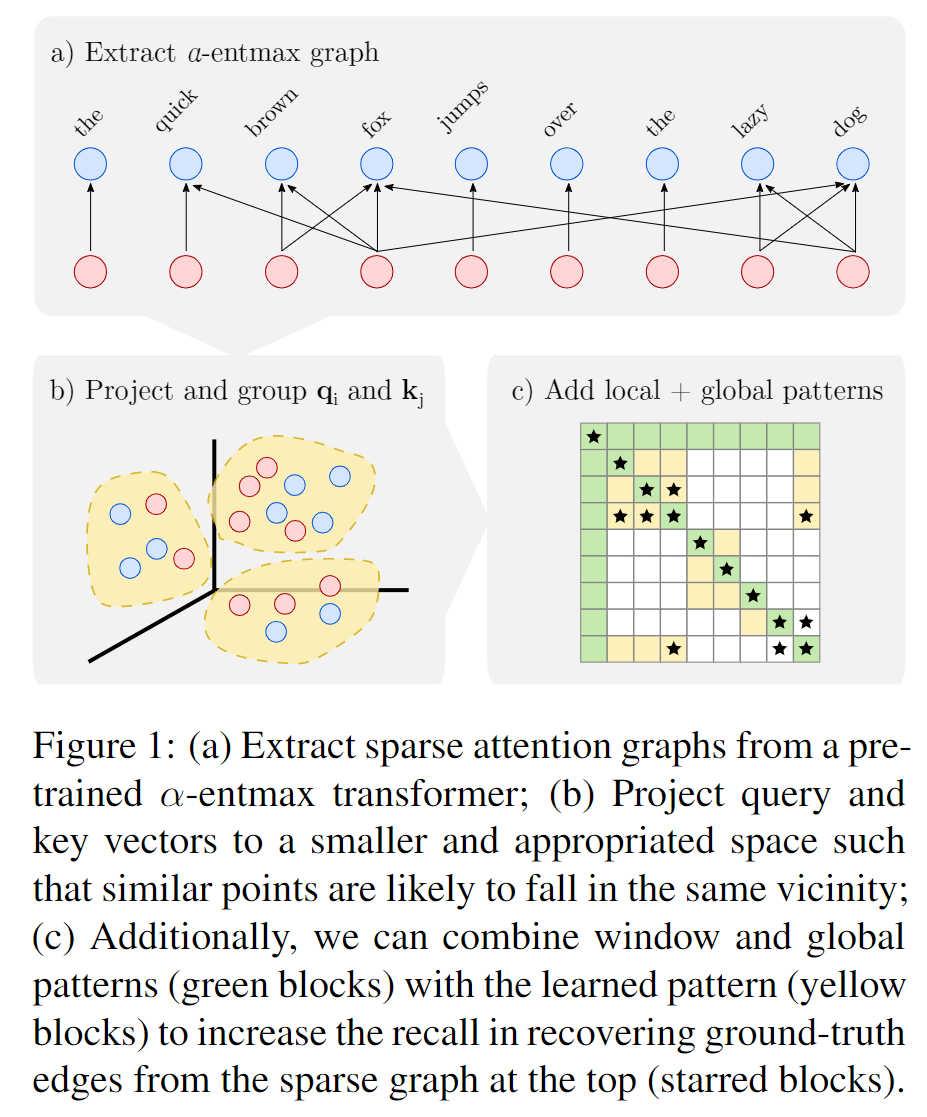
现在已经有不少基于稀疏性的方法来优化 Transformer 的时间空间复杂性是 $O(n^2)$ 的问题。但是这些操作需要一些额外的计算。
本文提出 Sparsefinder, 在这些额外计算之前就能获得到这种稀疏的 attention, Sparsefinder 包含基于三种方法的 1. metric learning 2. quantization 3. clustering

通过利用 α-entmax transformation， 替代 Softmax 来直接获得稀疏的 patterns。不需要像之前的那些提出的模型通过近似的方法来获得。

当 limit α →1 时，α-entmax 恢复成 Softmax, $\alpha>1$ 时，获得稀疏的表示。

Sparsefinder

对于每个 attention 的 head 来可以定义一个这样的图

$\mathcal{G}_{h}=\left\{\left(\mathbf{q}_{i}, \mathbf{k}_{j}\right) \mid p_{i, j}>0\right\}$

那我们要做的就是，预计出来的这个稀疏的图满足如下条件

$\operatorname{recall}\left(\hat{\mathcal{G}}_{h} ; \mathcal{G}_{h}\right)=\frac{\left|\hat{\mathcal{G}}_{h} \cap \mathcal{G}_{h}\right|}{\left|\mathcal{G}_{h}\right|}$

三种方法如下

可学习的参数映射，讲高维的 $\mathbf{q}, \mathbf{k} \in \mathbb{R}^{d}$ 映射到低维的 $\mathbf{q}^{\prime}, \mathbf{k}^{\prime} \in \mathbb{R}^{r}$ 使得 $r \ll d$, 最后使用对比学的方法来训练这些参数, Loss 定义如下。

$\mathcal{L}_{\theta}\left(\mathcal{G}_{h}\right)=\left[\omega+\left\|\mathbf{q}^{\prime}-\mathbf{k}_{\mathrm{P}}^{\prime}\right\|_{2}^{2}-\left\|\mathbf{q}^{\prime}-\mathbf{k}_{\mathrm{N}}^{\prime}\right\|_{2}^{2}\right]_{+}$

1. 通过距离来匹配 $\hat{\mathcal{G}}_{h}=\left\{\left(\mathbf{q}_{i}, \mathbf{k}_{j}\right) \mid\left\|\mathbf{q}_{i}^{\prime}-\mathbf{k}_{j}^{\prime}\right\|_{2} \leq t\right\}$ 也需要 $O(n^2)$ 但是由于 $r \ll d$ 所以会快得多。

2. Buckets through quantization 将每个维度量化为 $1, \ldots, r$ 然后放入 $\beta$ bins。有相关联的 query 和 key 就会被放进同个 bucket。

3. Buckets through clustering 使用 $k-means$ 分成不同的 bucket