Dark-Existed's Blog

Vanilla MLP

$O=\phi(XW_u)W_o$

GLU (Gated Linear Unit)

[[GLU Variants Improve Transformer]] 中提出的

$U=\phi_u(XW_u)$

$V=\phi_v(XW_v)$

$O=(U\odot V)W_o$

一般来说 GLU 中 $U$ 不加激活函数而 $V$ 加 Sigmoid，但是本篇论文 $U$ $V$ 都加了激活函数 Switch (Sigmoid Linear Unit)

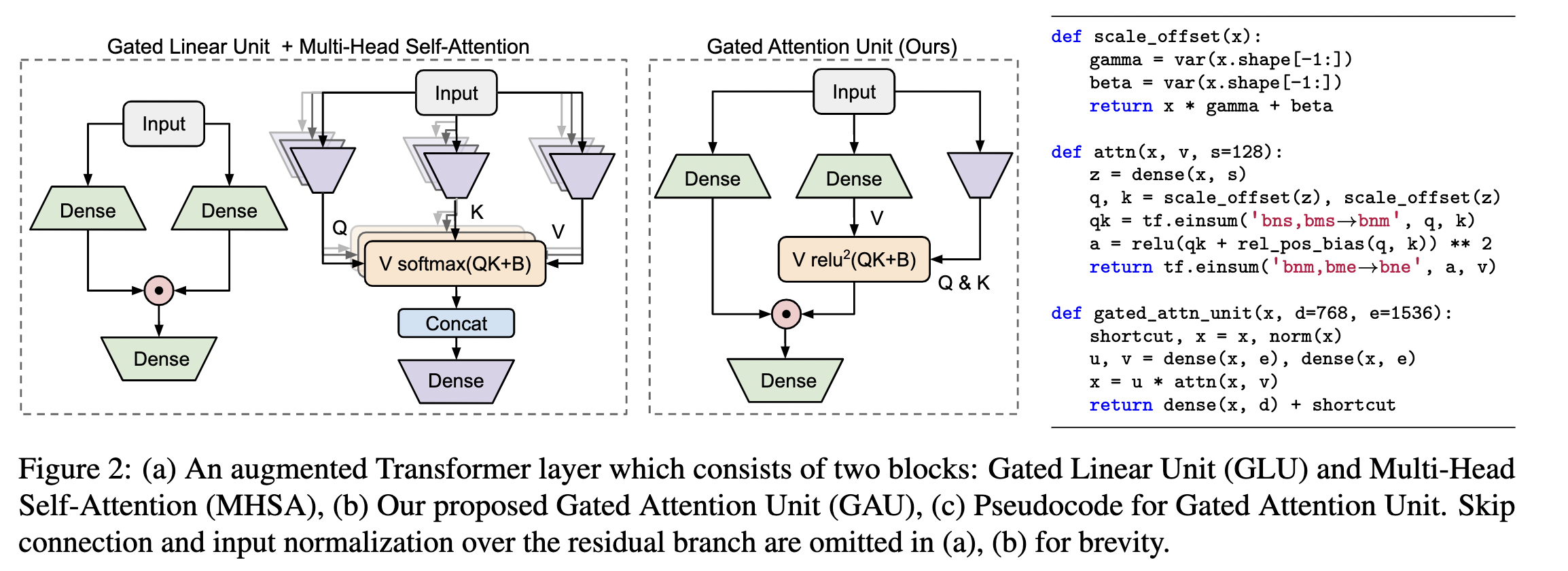
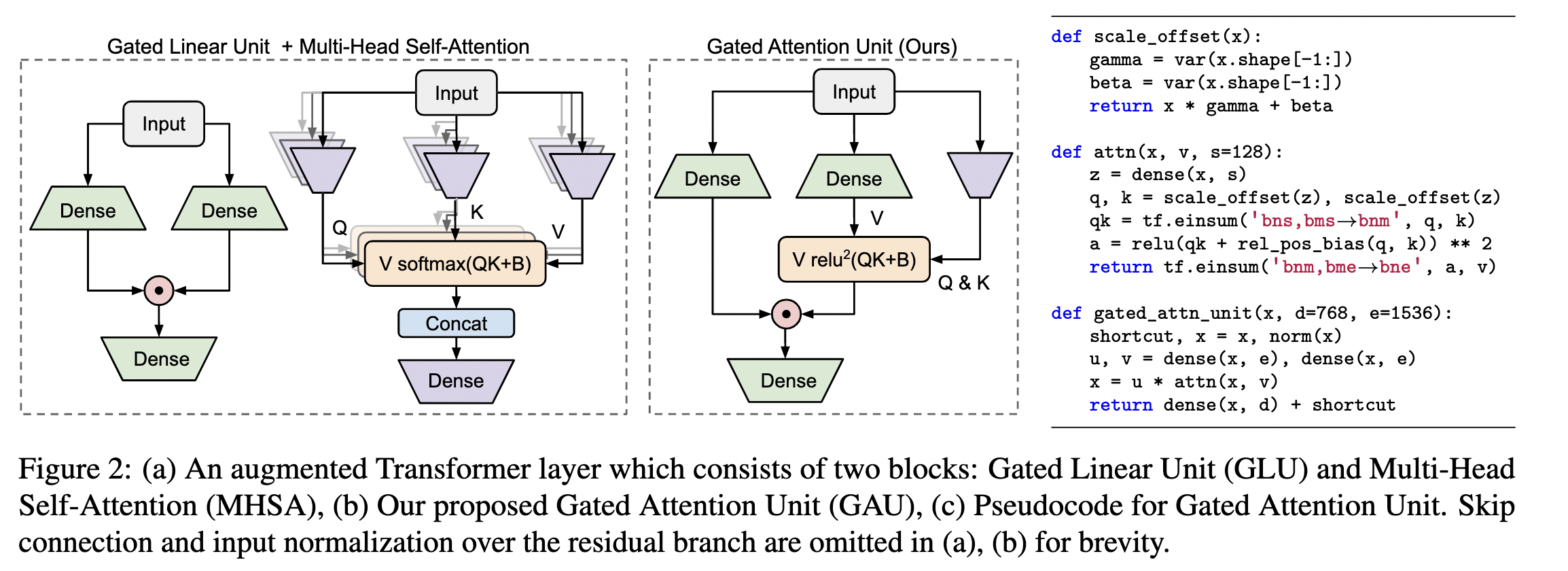
GAU

既然 GLU 形式的 FFN 更有效，就提出在此基础上进行修改。
FFN 不能取代 Attention，是因为它的各个 token 之间没有进行交互。也就是说 $U$ $V$ 是独立运算的，为了解决这个问题很自然的想法就是，把token 之间的联系补充到 $U$ $V$上。

$O=(U\odot AV)W_o$

由 $A$ 来融合 token 之间的信息。
如果 $A$ 等于 $I$ 那就是GLU形式的FFN，如果 $U$全是1矩阵，那么就是普通的注意力机制。

原论文使用了简化版的 Attention

$\boldsymbol{A}=\frac{1}{n} \operatorname{relu}^{2}\left(\frac{\mathcal{Q}(\boldsymbol{Z}) \mathcal{K}(\boldsymbol{Z})^{\top}}{\sqrt{s}}+b\right)=\frac{1}{n s} \operatorname{relu}^{2}\left(\mathcal{Q}(\boldsymbol{Z}) \mathcal{K}(\boldsymbol{Z})^{\top} + b\right), \quad \boldsymbol{Z}=\phi_{z}\left(\boldsymbol{X} \boldsymbol{W}_{z}\right)$

其中 $\mathcal{Q}$ $\mathcal{K}$ 是仿射变化 $s$为注意力的 head_size
$\frac{1}{n}$ 是作者团队之前 通过 NAS搜索出来的归一化因子，来消除长度的影响。

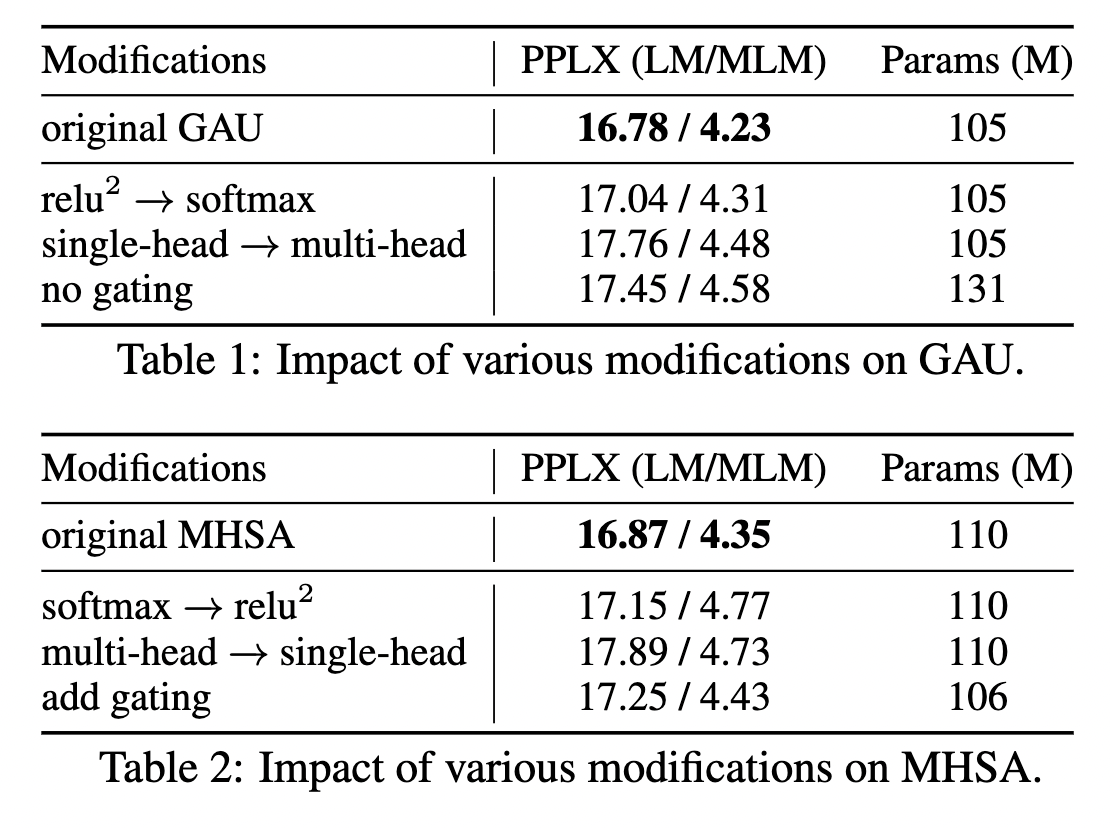
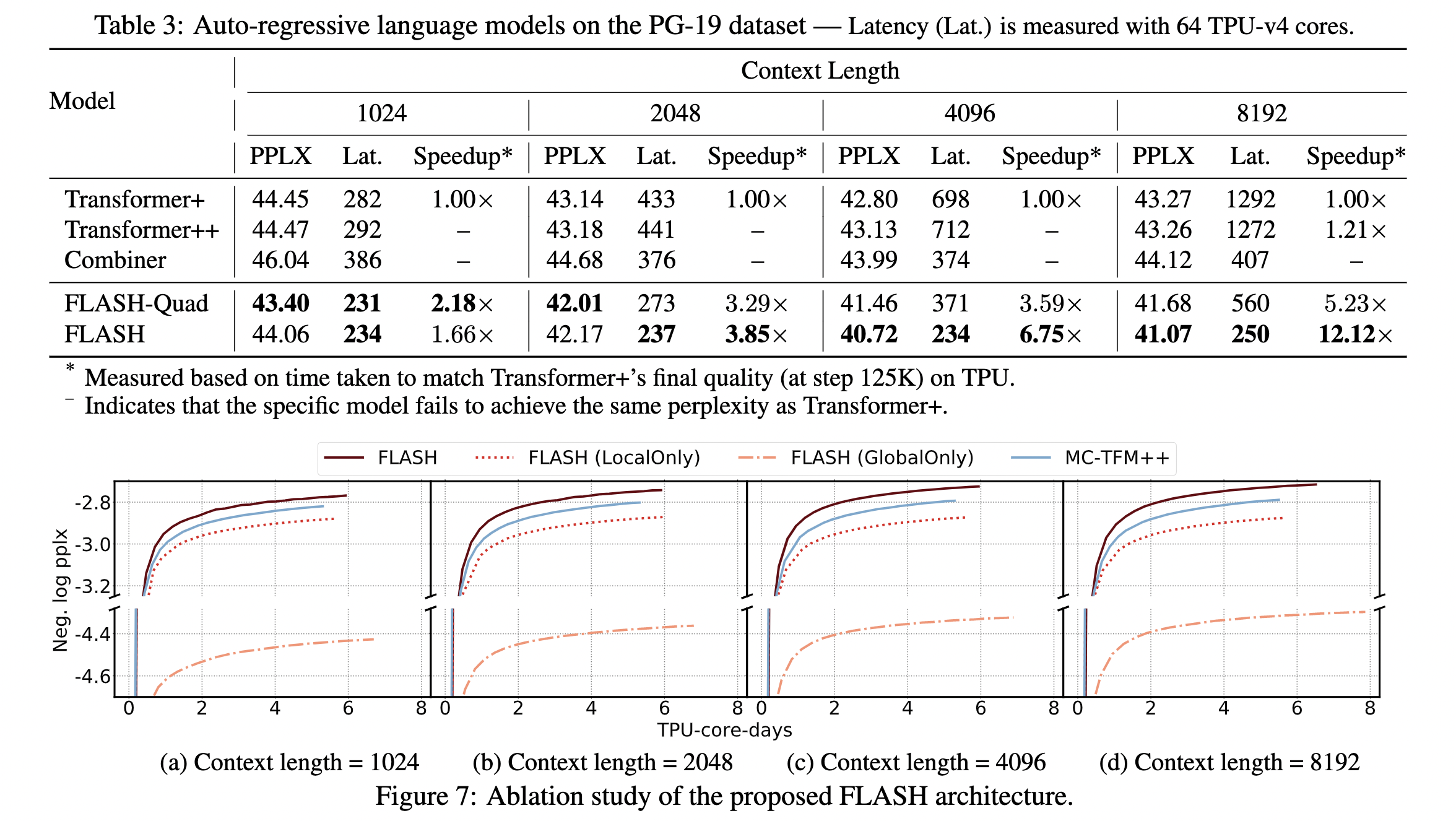
PPLX (perplexity): 刻画LM预测语言样本的能力，表示每个位置需要多少种类的词才能表示该句子 越小越好

可以看到 只用一个 head 时候效果也不错。

进一步降低复杂度

主要就两种途径

1. 稀疏化
2. 线性化

本文使用了 分块-混合的方法，融合了局部和全局的特征。
对于长度为 n 的序列，按长度 c 分为 $\frac{n}{c}$ 块。

$\hat{\boldsymbol{V}}_{g}^{\text {quad }}=\frac{1}{c s} \operatorname{relu}^{2}\left(\boldsymbol{Q}_{g}^{\text {quad }} \boldsymbol{K}_{g}^{\mathrm{quad}^{\top}}+b\right) \boldsymbol{V}_{g}$

$g$ 为第$g$块

$\hat{\boldsymbol{V}}_{g}^{\operatorname{lin}}=\frac{1}{n} \boldsymbol{Q}_{g}^{\operatorname{lin}} \sum_{h=1}^{n / c} \boldsymbol{K}_{h}^{\operatorname{lin}^{\top}} \boldsymbol{V}_{h}$

然后将两种 Attention 结合起来

$\boldsymbol{O}_{g}=\left[\boldsymbol{U}_{g} \odot\left(\hat{\boldsymbol{V}}_{g}^{\text {quad }}+\hat{\boldsymbol{V}}_{g}^{\text {lin }}\right)\right] \boldsymbol{W}_{o}$